Myers Diff Algorithm - Code & Interactive Visualization
Below you will find example source code and interactive visualizations that are intended to complement the paper 'An O(ND) Difference Algorithm and Its Variations' by Eugene W. Myers[1]. Multiple variants of the algorithms discussed in Myers' paper are presented in this article, along with working source code versions of the pseudo-code presented in the paper.
Two refinements to the linear-space Myers algorithm are also discussed. These refinements reduce the memory requirements of the classical algorithm from O(len(a) + len(b)) to O(min(len(a),len(b))), and the worst-case execution-time requirements from O((len(a) + len(b)) * D) to O(min(len(a),len(b)) * D). Finally, a proof-of-concept patch for GNU diffutils is included that produces slower execution for many typical use cases, but is asymptotically superior as the size difference between the files grows arbitrarily large when calculating the minimum edit difference.
Linear Space Myers Diff Algorithm Python Code
def diff(e, f, i=0, j=0): N,M,L,Z = len(e),len(f),len(e)+len(f),2*min(len(e),len(f))+2 if N > 0 and M > 0: w,g,p = N-M,[0]*Z,[0]*Z for h in range(0, (L//2+(L%2!=0))+1): for r in range(0, 2): c,d,o,m = (g,p,1,1) if r==0 else (p,g,0,-1) for k in range(-(h-2*max(0,h-M)), h-2*max(0,h-N)+1, 2): a = c[(k+1)%Z] if (k==-h or k!=h and c[(k-1)%Z]<c[(k+1)%Z]) else c[(k-1)%Z]+1 b = a-k s,t = a,b while a<N and b<M and e[(1-o)*N+m*a+(o-1)]==f[(1-o)*M+m*b+(o-1)]: a,b = a+1,b+1 c[k%Z],z=a,-(k-w) if L%2==o and z>=-(h-o) and z<=h-o and c[k%Z]+d[z%Z] >= N: D,x,y,u,v = (2*h-1,s,t,a,b) if o==1 else (2*h,N-a,M-b,N-s,M-t) if D > 1 or (x != u and y != v): return diff(e[0:x],f[0:y],i,j)+diff(e[u:N],f[v:M],i+u,j+v) elif M > N: return diff([],f[N:M],i+N,j+N) elif M < N: return diff(e[M:N],[],i+M,j+M) else: return [] elif N > 0: return [{"operation": "delete", "position_old": i+n} for n in range(0,N)] else: return [{"operation": "insert", "position_old": i,"position_new":j+n} for n in range(0,M)]
Some examples of how to make use of this function are provided later in this article. If you find the above code a bit cryptic the interactive explanation below should help:
M = length('abcoeppklmn') = 11
N = length('op') = 2
MAX = M + N = 13
D=0D=1D=0k=-1(11,3)(0,0)(0,1)(0,2)(1,0)(1,1)(1,2)(2,0)(2,1)(2,2)(3,0)(3,1)(3,2)(4,0)(4,1)(4,2)(5,0)(5,1)(5,2)(6,0)(6,1)(6,2)(7,0)(7,1)(7,2)(8,0)(8,1)(8,2)(9,0)(9,1)(9,2)(10,0)(10,1)(10,2)(11,0)(11,1)(11,2)abcoeppklmnop?001??-2-10123Best X Values (forward)V[(k+2)%6-2](k+2)%6-2??00??-2-10123Best X Values (reverse)V[(k+2)%6-2](k+2)%6-2V[-1] = V[-1 + 1]Add insertion to path.Add insertion to path.
The visualization above incorporates a number of different ideas and neologisms, and you many have to do a quick read of the original paper[1] to fully grasp all of them. In addition, a couple optimizations not discussed in the paper are also described below. Let's start from the beginning, and understand this algorithm from scratch:
The first step is easy to understand, and it involves laying out a grid that allows us to compare different subsections of the two sequences we want to compare.
(0,0)(0,1)(0,2)(0,3)(0,4)(0,5)(0,6)(1,0)(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)(2,0)(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)(3,0)(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)(4,0)(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)(5,0)(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)(6,0)(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)(7,0)(7,1)(7,2)(7,3)(7,4)(7,5)(7,6)abcabbacbabac
Diagonal lines are used to represent items that match.
Edit Script = 1D, 1Ic, 2Iaba, 4D, 5D, 6D, 7D
DeleteInsertUnchanged(0,0)(0,1)(0,2)(0,3)(0,4)(0,5)(0,6)(1,0)(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)(2,0)(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)(3,0)(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)(4,0)(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)(5,0)(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)(6,0)(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)(7,0)(7,1)(7,2)(7,3)(7,4)(7,5)(7,6)abcabbacbabac
It is now possible to describe any edit sequence that transforms the first sequence into the second one, by simply describing a path through this graph from the top left-hand corner to the bottom right. All paths between these two points correspond to valid edit sequences. Some paths are more preferable than others.
k=0k=1k=-1k=2k=-2k=3k=-3(0,0)(0,1)(0,2)(0,3)(0,4)(0,5)(0,6)(1,0)(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)(2,0)(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)(3,0)(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)(4,0)(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)(5,0)(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)(6,0)(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)(7,0)(7,1)(7,2)(7,3)(7,4)(7,5)(7,6)abcabbacbabac
An important part of algorithms described in Myers' paper involves the lines defined by k = x - y. These are important because any edit sequence that touches a given k line must have at least |k| insertions or deletions.
M = length('abcabba') = 7
N = length('cbabac') = 6
MAX = M + N = 13
D=0D=1k=0(0,-1)(0,0)(0,1)(0,2)(0,3)(0,4)(0,5)(0,6)(1,0)(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)(2,0)(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)(3,0)(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)(4,0)(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)(5,0)(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)(6,0)(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)(7,0)(7,1)(7,2)(7,3)(7,4)(7,5)(7,6)abcabbacbabac???????????2001????????????-13-12-11-10-9-8-7-6-5-4-3-2-1012345678910111213Best X Values (forward)V[k]kV[0] = V[0 + 1]Add insertion to path.Add insertion to path.
The above visualization shows the basic algorithm working to find the shortest path. Note that the algorithm depicted above is only finding the length of the shortest edit script using a linear amount of space. In order to recover the full path this variant of the algorithm would require O(D^2) space to recover the full path. This polynomial space requirement is reduced to a linear space requirement as shown in step 6.
M = length('abcabba') = 7
N = length('cbabac') = 6
MAX = M + N = 13
D=0D=1D=0k=-1(7,7)(0,0)(0,1)(0,2)(0,3)(0,4)(0,5)(0,6)(1,0)(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)(2,0)(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)(3,0)(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)(4,0)(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)(5,0)(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)(6,0)(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)(7,0)(7,1)(7,2)(7,3)(7,4)(7,5)(7,6)abcabbacbabac????????????001????????????-13-12-11-10-9-8-7-6-5-4-3-2-1012345678910111213Best X Values (forward)V[k]k?????????????00????????????-13-12-11-10-9-8-7-6-5-4-3-2-1012345678910111213Best X Values (reverse)V[k]kV[-1] = V[-1 + 1]Add insertion to path.Add insertion to path.
As discussed in the previous section, the naive implementation for recovering the full edit path would require O(D^2) space. This is not very scalable, but fortunately there is a divide and conquer approach that only requires linear space (shown above). This approach runs the same distance measuring algorithm described in the last section, but it runs simultaneously from both ends of the edit graph. When they meet in the center, the algorithm is repeatedly run on the two smaller sub-sections. This gets repeated until the sub-regions end up being trivial base cases that are simply insertions or deletions.
M = length('abgdef') = 6
N = length('gh') = 2
MAX = M + N = 8
D=0D=1D=0k=-1(6,3)(0,0)(0,1)(0,2)(1,0)(1,1)(1,2)(2,0)(2,1)(2,2)(3,0)(3,1)(3,2)(4,0)(4,1)(4,2)(5,0)(5,1)(5,2)(6,0)(6,1)(6,2)abgdefgh???????001???????-8-7-6-5-4-3-2-1012345678Best X Values (forward)V[k]k????????00???????-8-7-6-5-4-3-2-1012345678Best X Values (reverse)V[k]kV[-1] = V[-1 + 1]Add insertion to path.Add insertion to path.
This step illustrates the benefit you get by restricting the bounds of k more intelligently. This step is discussed in more detail later in this article.
The Basic Algorithm
In the descriptions above, there are really two different algorithms being shown. The first is shown in step 5. This is the basic algorithm which only calculates the length of the shortest edit script. Step 6 shows the second version which applies the same algorithm in step 5, but in both directions. Here is Python code for the first version shown in step 5:
def shortest_edit_script_length(old, new): N = len(old) M = len(new) MAX = N + M V = [None] * (2 * MAX + 2) V[1] = 0 for D in range(0, MAX + 1): for k in range(-D, D + 1, 2): if k == -D or k != D and V[k - 1] < V[k + 1]: x = V[k + 1] else: x = V[k - 1] + 1 y = x - k while x < N and y < M and old[x] == new[y]: x = x + 1 y = y + 1 V[k] = x if x >= N and y >= M: return D
The above algorithm is described as pseudo code on page 6 of Myers' original paper[1]. It works by iteratively trying to find paths with the highest x value on each k line for successively higher edit distances.
In the original paper this version of the algorithm is depicted as 'running off' the edit grid, and thus requires twice as much memory (and worst-case execution time) as it needs to. Here is a version of this algorithm that only requires half the memory:
def myers_diff_length_half_memory(old, new): N = len(old) M = len(new) MAX = N + M V = [None] * (MAX + 2) V[1] = 0 for D in range(0, MAX + 1): for k in range(-(D - 2*max(0, D-M)), D - 2*max(0, D-N) + 1, 2): if k == -D or k != D and V[k - 1] < V[k + 1]: x = V[k + 1] else: x = V[k - 1] + 1 y = x - k while x < N and y < M and old[x] == new[y]: x = x + 1 y = y + 1 V[k] = x if x == N and y == M: return D
Since the algorithm works by moving diagonally from the top left corner to the bottom right corner, the original version checks all k lines in the range of -D to D because these are the only k lines that can be reached in D edits. However, once the algorithm begins to follow k lines as they touch the bottom or right-hand boundary of the edit graph, we know for sure that no k line that is less than, or greater than, respectively, will be able to produce a shorter edit path. If it could, this would be a contradiction since it would necessarily need to overlap the current best path. In addition to using less memory, this version will also search far fewer points in the worst case. Also note that the finish condition can now be changed to use equality instead of greater than or equal to.
Note that, once again, this version of the algorithm only calculates the length of the shortest edit sequence. The second version of this algorithm that we'll review in a moment, runs the search from both directions at the same time, and this optimization can also have some benefit there too.
Linear Space Edit Script Recovery
In the previous section we reviewed the basic algorithm for calculating the length of the shortest edit script for a pair of sequences. If you were to adapt the basic algorithm to allow you to recover the full edit script, you would need to store the entire 'best path' for each k line instead of just storing a single number that represents how far you can reach on that k line. This would require O(D^2) space.
Instead of storing 'best paths' and discarding them when they are proved inferior, we can instead simply run the same length calculation simultaneously in both directions at the same time. When they meet in the middle, we can run the algorithm recursively on the two smaller sub-sections. This is shown in step 6 above. In addition, we can also apply the optimization discussed previously where we restrict the bounds on k so that we don't let paths fall off the edit grid. This is shown in step 7 above. A final optimization for cases where the sequences are of different length can be made by only allocating enough memory to span the k lines of whichever sequence is smaller. Since the size of the edit grid can be asymmetric, we can consider the V array to act as thought it were a circular buffer and re-cycle space from k lines that will never be checked again. This final optimization is shown in step 8 above. These last two optimizations take the worst-case execution time from O((len(a) + len(b))*D) to O(min(len(a),len(b)) * D). The space requirements are reduced from O(len(a) + len(b)) to O(min(len(a),len(b))).
One additional benefit of these two potential refinements is that they should have no effect at all on the output compared to that of the original algorithm. This would make unit testing for correctness much easier when adapting existing implementations.
Is The Recursive Myers Algorithm Optimal?
An important question worth asking is "Does the Myers algorithm find the shortest possible edit path through the grid?". It is also important to note that there can be multiple shortest paths through the edit grid. The paper provides a proof that supports the claim that it does find (one of) the shortest possible paths. The paper provides this claim for the basic algorithm, as well as the linear space recursive version. The non-recursive greedy algorithm for finding the shortest path seem a bit more intuitively optimal, but I wasn't sure about the recursive one so I did a bit of digging. I ended up finding the following write-up by Neil Fraser that contains an example that, for a while, had me convinced that the recursive algorithm wasn't optimal and that the original paper might have had an error in it:
M = length('xaxcxabc') = 8
N = length('abcy') = 4
MAX = M + N = 12
D=0D=1D=0k=-1(8,5)(0,0)(0,1)(0,2)(0,3)(0,4)(1,0)(1,1)(1,2)(1,3)(1,4)(2,0)(2,1)(2,2)(2,3)(2,4)(3,0)(3,1)(3,2)(3,3)(3,4)(4,0)(4,1)(4,2)(4,3)(4,4)(5,0)(5,1)(5,2)(5,3)(5,4)(6,0)(6,1)(6,2)(6,3)(6,4)(7,0)(7,1)(7,2)(7,3)(7,4)(8,0)(8,1)(8,2)(8,3)(8,4)xaxcxabcabcy???????????002???????????-12-11-10-9-8-7-6-5-4-3-2-10123456789101112Best X Values (forward)V[k]k????????????00???????????-12-11-10-9-8-7-6-5-4-3-2-10123456789101112Best X Values (reverse)V[k]k...Can only go up, since k == -DCan only go up, since k == -D
Of course, you can just play the animation above to see what happens, but before I had written this myself, I followed through the algorithm and found that the blog post had a good point! If you follow the recursive Myers algorithm as described in the paper the first paths to intersect are not optimal! The thing is, in this example the algorithm doesn't choose the first pair of 'best paths' that overlap. Instead, it finds the first snake on a pair of overlapping k lines that have 'best x values' that sum to be greater than the length of the first sequence (or some equivalent condition). If you think about this for a bit, you realize that this implies that either the paths do overlap, or that you could use the two non-overlapping paths to build an overlapping path with less than or equal to the same number of edits. You only need to check for a 'best x value' in the opposing direction's k line that is capable of touching your 'best x value' in the current k line.
In conclusion, Yes, both the basic algorithm, and the recursive Myers diff algorithms are optimal. Optimal means that they find at least one of the (possibly many) shortest possible edit scripts to produce the second sequence from the first. I was able to convince myself that these algorithms are optimal by doing a few hours of randomized testing with randomly created sequences of varying lengths, and comparing their results with the basic algorithm. I also added a check to generate a random valid edit path, and make sure it was greater than or equal to in length than the two other algorithms. Finally, there are also various complementary relationships that I checked such as the relationship between the number of items in the longest common subsequence, the number of edits in the shortest edit script, and the length of the sequences. You can find the source code for these test and many variants of the Myers algorithms here.
What Is A Snake?
One really important concept for understanding Myers' paper is understanding the concept of a 'snake'. The paper defines a snake as follows: "Let a D-path be a path starting at (0,0) that has exactly D non-diagonal edges. A 0-path must consist solely of diagonal edges. By a simple induction, it follows that a D-path must consist of a (D − 1)-path followed by a non-diagonal edge and then a possibly empty sequence of diagonal edges called a snake." Unfortunately, this definition of a snake is not clearly worded. Given only this statement, I would understand a 'snake' to mean one of the following possible things:
-
- A snake is a possibly empty sequence of diagonal edges that does not contain horizontal edges or vertical edges.
-
- A snake is a non-diagonal edge followed by a possibly empty sequence of diagonal edges.
-
- A snake is a D-path followed by a non-diagonal edge followed by a possibly empty sequence of diagonal edges.
Having spent a lot of time considering this question, I am of the opinion that option #1 is the most correct interpretation. I have seen other writings online that suggest that definition #2 is the correct interpretation, but I disagree with this. Here are a few quotes that appear elsewhere in the paper that lead me to this conclusion: "As noted before, a D-path consists of a (D − 1)-path, a non-diagonal edge, and a snake.", "A 0-path must consist solely of diagonal edges.", "A D-path has D+1 snakes some of which may be empty.".
Furthermore, defining a snake as a "possibly empty sequence of diagonal edges" is not a very convenient formal definition, since one of our algorithms requires 'finding the middle snake' of an edit path and returning it. When the middle snake is an empty sequence of edges, there isn't anything to return, but we do need to distinguish between different empty middle snakes, because they have different origin points associated with them. Therefore, I will offer an alternative definition of what a snake is: A snake is an ordered sequence of one or more points ((x_1, y_1), (x_2, y_2), (x_3, y_3),...) where x_(n+1) = x_n + 1 and where y_(n+1) = y_n + 1.
Minimal Edit Scripts and Longest Common Subsequence
The paper discussed an intimate relationship between the problem of finding (one of) the shortest edit scripts, and (one of) the longest common sub-sequences. If you think about it, you could find the longest common sub-sequence between two sequences by finding the shortest edit script, then simply replaying all the deletions, but discarding any insertions.
It should then come as no surprise that most of the heavy lifting for the recursive Myers algorithm and the problem of finding the longest common subsequence is actually done using a common algorithm. This algorithm is the 'find middle snake' algorithm discussed in the paper, and you can find source code for it here on GitHub.
The paper also mentions a somewhat non-intuitive relationship between edit script length, sequence length, and longest common subsequence: D = N+M−2L, where D is the length of the shortest edit script (composed of delete or insert statements), N is the length of the first sequence, M is the length of the second sequence, and L is the length of the longest common subsequence. Similarly, L is the number of diagonal edges that occur in the path described by the shortest edit sequence.
Python Source Example
As promised above, here is an example of how you could make use of the python code found in the introduction:
NOTE s1 = ["apple","orange","pear"] s2 = ["apple","orange","blueberry", "potato"] result = diff(s1, s2) print(str(result))
The output for this code will be the following:
[{'operation': 'insert', 'position_new': 2, 'position_old': 2}, {'operation': 'insert', 'position_new': 3, 'position_old': 2}, {'operation': 'delete', 'position_old': 2}]
You can use this to produce a spoken-word description of how to edit the first sequence to become the second one:
def print_edit_sequence(e, s1, s2): for e in es: if e["operation"] == "delete": print("Delete " + str(s1[e["position_old"]]) + " from s1 at position " + str(e["position_old"]) + " in s1.") else: print("Insert " + str(s2[e["position_new"]]) + " from s2 before position " + str(e["position_old"]) + " into s1.") s1 = ["apple","orange","pear"] s2 = ["apple","orange","blueberry", "potato"] es = diff(s1,s2) print_edit_sequence(es, s1, s2)
The result of running this code will be:
Insert blueberry from s2 before position 2 into s1. Insert potato from s2 before position 2 into s1. Delete pear from s1 at position 2 in s1.
Finally, here is an example of an algorithm for actually applying the edit sequence to s1 in order to fully re-produce s2:
def apply_edit_script(edit_script, s1, s2): i, new_sequence = 0, [] for e in edit_script: while e["position_old"] > i: new_sequence.append(s1[i]) i = i + 1 if e["position_old"] == i: if e["operation"] == "delete": i = i + 1 elif e["operation"] == "insert": new_sequence.append(s2[e["position_new"]]) while i < len(s1): new_sequence.append(s1[i]) i = i + 1 return new_sequence s1 = ["apple","orange","pear"] s2 = ["apple","orange","blueberry", "potato"] es = diff(s1, s2) new_sequence = apply_edit_script(es, s1, s2) print(str(new_sequence))
In the above example, you could eliminate the need for keeping s2 by changing the diff function (or its return value) to include the inserted element from s2 instead of just the position where it came from in s2.
Patching Diffutils
As noted above, there are a couple potential optimizations that aren't described in Myers' paper. I figured it was worth checking out two well-known pieces of software (diff and git) that are known to use this algorithm and see if they could take advantage of these optimizations. The 'optimizations' described above will technically give a small constant factor slowdown in the worst-case scenario, but still have identical memory requirements in this case. In the best case, these optimizations will reduce the memory requirements of the search algorithm from len(a) + len(b) to 2*min(len(a),len(b)), and decrease the execution time from a quadratic amount toward a linear amount as the ratio of min(len(a),len(b)) / max(len(a),len(b)) tends toward zero. Note that the memory advantage discussed does not include the memory required to actually represent the sequences themselves, which is likely to be much larger than the memory required by the Myers algorithm.
Upon closer inspection, both git[2] and diff[3], appear to allocate memory based on the sum of the sequence lengths, instead of the minimum sequence length. Furthermore, they also appear to let the calculations run off the end of the edit grid as described in the paper.
Therefore, I decided to create a patch for diffutils and see if I could demonstrate any performance benefits. The testing method I used was to create files containing various numbers of lines containing random numbers, and then measure how the performance scaled based on how many lines were in the files. The command I used to generate the files with random data was the following command:
hexdump -e '2/1 "%02x " "\n"' /dev/urandom | head -n NUMBER_OF_LINES
I will highlight the results from two different perspectives: The first will be to show the 'Worst Case' performance difference of the patched vs. unpatched in the scenario where no speedup or memory advantage was expected. In this case, the extra calculations to do bounds checking will even cause some amount of slowdown. Furthermore, when running diff without the --minimal flag, diff actually uses a slightly faster heuristic which skips parts of the Myers algorithm and does not produce a minimal difference, but gives a better run time.
The second perspective will highlight the 'best case' benchmarks results for a case that specifically favours the changes made in the patch: Using the --minimal flag to generate a minimum difference in the case where the size of the two files is very different.
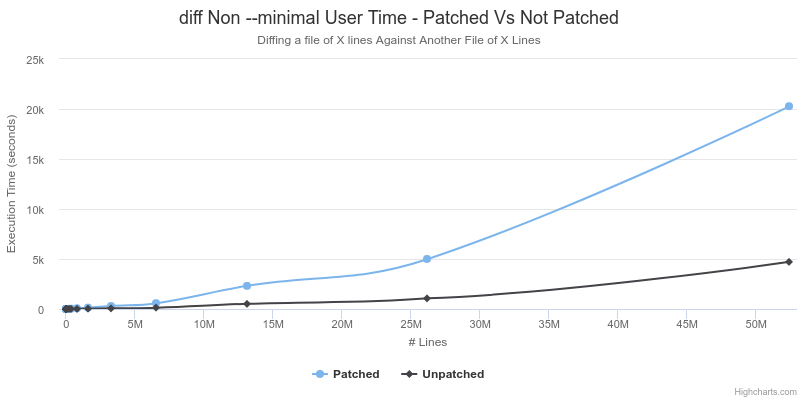 | 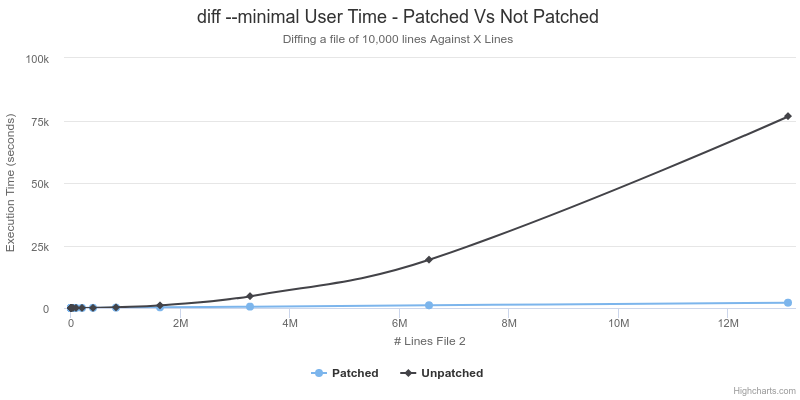 |
As shown above, the patched version of diff runs slower by a roughly constant factor of about 5 on cases where it was not expected to encounter any speedup. However, in the case where the files are of significantly different size, and diff is instructed to calculate a minimal difference, the asymptotic run-time is better with the patched version. The unpatched version exhibits a run time that is quadratic in relation to the size of the second file, whereas the patched version has an almost perfectly linear relationship. This supports the previous analysis described above about the 2 additional refinements to the Myers algorithm.
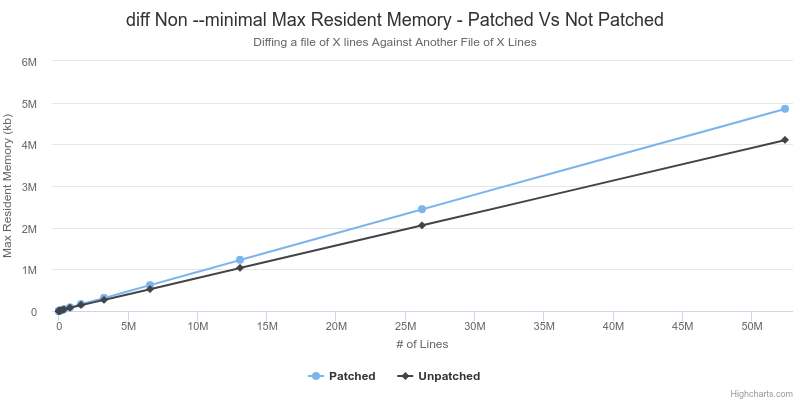 | 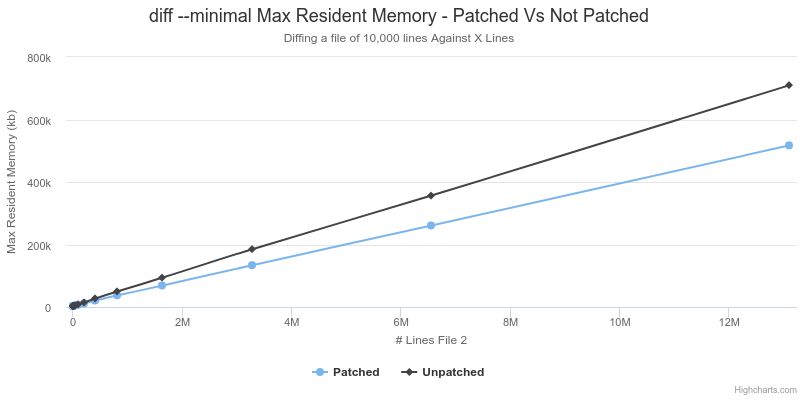 |
As shown above, the patched version of diff empirically has a higher max resident memory size. This is not expected since the patched version of diff should have the same memory requirements when len(a) == len(b), but less in any other case. I did not investigate this too closely, I suspect that it may be related to the I/O operations that diff needs to perform. Perhaps the longer run time causes it to encounter different behaviour related to the kernel caching data from disk?
In the best case situation the calculated memory savings for the last data point based on the changes in the patch would be ((13107200 + 10000) * 2 * 8) - ((2 * 10000) * 2 * 8) = 209,555,200 bytes. The observed difference above is (710056 - 517380) * 1024 = 197,300,224 bytes. These figures are close enough that I will attribute the small difference to noise and suggest that this supports the analysis above about decreased memory requirements.
The information above was collected using '/usr/bin/time -v'. In all cases, the outputs were compared and verified to be identical. I also tested with a few hundred randomized inputs both with and without --minimal using testing code that can be found in with various other Myers algorithm variations. I was unable to find a case where the outputs were different, or there was a valgrind error reported. The patch passes the 'make check' unit tests in diffutils, but I don't trust them, as they were still all able to pass even when I broke the Myers diff algorithm horribly.
In conclusion, if it were possible to improve this patch so that the extra bounds calculation and modulo arithmetic of the array access had a negligible cost, then this patch might be worth applying. If you had the rather specific need to calculate a minimal difference set from an relatively small file against a relatively large file, then this patch would be unquestionably better. I only stopped the minimal difference benchmarks where I did because the next run-time data points for doubling the file size with the unpatched version would have a progression of taking ~4 days, ~16 days, ~64 days..., whereas the patched version would take ~1 hour, ~2 hours, ~4 hours etc. I don't have a good explanation for the increased memory usage in the worst case scenario with the patched version, but the changes to the algorithm don't imply more memory should ever be used. I haven't tried particularly hard to optimize this code, and in cases where I did test small adjustments that I thought would improve things, I ended up slowing down execution by 10 times! Clearly, this is a piece of code where the influence of cache lines, instruction pipelining and branch prediction are worth considering. Having said this, I don't plan to continue working on the patch, but if someone else wants to then I'm all for it.
Also, here is the raw data listed above:
|
|
More Details
This article has been written with an emphasis on augmenting the explanation found in the original paper. There were a few things I would have personally simplified myself, but I stuck with keeping many things as close to the original paper as I could. In addition, the next few paragraphs contain a few miscellaneous details that I had to figure out when I was reading the original paper.
The V array in the paper contains the elements from 1 to MAX because it must be capable of expressing the worst-case edit script where everything is deleted in A, then everything from B is inserted. The elements from -1 to -MAX are needed to represent the worst-case edit sequence in the opposite order: Insert everything from B, then deleting everything in A. As seen above, the size of this array can be reduced by restricting the range of k values, and also using the array as a circular buffer.
One of the challenges I had in understanding the basic algorithm was trying to figure out what this part was doing:
if k == -D or k != D and V[k - 1] < V[k + 1]: x = V[k + 1] else: x = V[k - 1] + 1
Here is another version of the same thing re-written to be a bit more clear:
if k == -D x = V[k + 1] elif k == D: x = V[k - 1] + 1 elif V[k - 1] < V[k + 1]: x = V[k + 1] elif V[k - 1] == V[k + 1]: x = V[k - 1] + 1 elif V[k - 1] > V[k + 1]: x = V[k - 1] + 1
Take note that when D == 0, then k == -D and k == D, so the ordering of the if statements is important. Another question I wondered when reviewing this code, is why does the calculation only add '+ 1' when choosing V[k - 1] and not when choosing k[k + 1]? The answer is related to the fact that the V array stores the 'best x values' and the equation x - y = k described in the paper. If we take V[k - 1] we're incrementing x by adding a deletion to the path. Therefore, we explicitly increment the x value. When we take V[k + 1], we're incrementing the y variable (an insertion) implicitly by taking the x value from a k line that is a distance of 1 away. Since x - y = k, the increment to the y variable happens implicitly by taking the x value from the neighbouring k line.
If you plan on just skimming the paper note that 'N' is used ambiguously in two different contexts the paper. In the introduction and title, 'N' is defined as being len(string a) + len(string b). Later, N is re-defined to be len(string b) and used repeatedly after this point.
A Warning About Portability And Modulus
The Myers algorithms and variants make heavy use modular arithmetic, and it's worth pointing out that the '%' operator does not do the same thing in every language. For example this python code:
print(str(-1 % 5))
will output the following:
4
but this C code will output the following:
#include <stdio.h> int main(void){ printf("%d\n", -1 % 5); }
will output the following:
-1
Please make sure you tell your children about the dangers of modular arithmetic and negative numbers.
Conclusion
In conclusion, the Myers diff algorithm was reviewed in detail using several interactive visualizations. There were two main variants of this algorithm: The first was a simple algorithm to calculate the length of a minimal edit script, and the second was a recursive divide-and-conquer approach to recovering the full edit sequence using only linear space. Also discussed were two refinements to the Myers diff algorithm that reduce the worst-case execution time from O((len(a) + len(b))*D) to O(min(len(a), len(b))*D) and the space requirements from O(len(a) + len(b)) to O(min(len(a),len(b))).
In addition, a patch for GNU diffutils was reviewed that empirically provides better asymptotic run time when calculating a minimal difference between a relatively large file and a relatively small file, but has overall worse performance when run on more typical non--minimal flag inputs. The patch could probably be improved to make this disadvantage go away, but I have no plans to work on this.
Multiple variants of the Myers algorithms and the diffutils patch are available here on GitHub.
References
[1] Here are a number of links in case some of them go dead: PDF Link 1, PDF Link 2, DOI: 10.1007/BF01840446
[2] A potential improvement in Git: Link To Git Source
[3] A potential improvement in Unix diff: Link To Diff Source
| Privacy Policy |
|