Causal Forecasting at Lyft (Part 2)
By Sameer Manek and Duane Rich
In our last blog, we discussed how managing our business effectively comes down to, in large part, making causally valid forecasts based on our decisions. Such forecasts accurately predict the future while still agreeing with experiment (e.g. increasing prices by X will decrease conversion by Y). With this, we can optimize our decisions to yield a desirable future.
But there remains a gap between theory and the implementation that makes it a reality. In this blog, we will discuss the design of software and algorithms we use to bridge this gap.
Problems Between Theory and Application
A powerful way to reason is to imagine the end state and enumerate the issues anticipated along the way. Our goal is a causally-valid forecasting system that predicts the whole of our business. As mentioned, there are theoretical advantages to framing this as a DAG of DAGs, each of which represents some input/output mapping from one set of variables to another.
From here, it’s clear we need to enable data scientists to develop models in parallel and combine them later using some protocol to guarantee compatibility and accuracy. Given the complexity of our business, we consider this modeling parallelism a hard requirement.
We also require useful aggregations. We know, apriori, it’s impossible to model bottom-up from the session-level to the national net revenue level. This necessitates a metrics framework that anticipates the use of sums and averages to measure our business’s most important dimensions. Doing so alleviates issues of computational tractability upfront.
Next, we should anticipate the model development cycle. Any high quality model of a complex mechanism follows a long sequence of iterations. When time and attention are constrained, a fast iteration cycle becomes a requirement. In implementation, this means models need to be easily declared and evaluated.
Finally, we must consider the final output: our decisions. These take the form of decisions optimized to produce desirable forecasts. To this end, there are several requirements. First, our software should assure us that whatever set of models we develop, we can optimize their potentially high-dimensional inputs. Further, we require a mechanism for evaluating counterfactual historical decisions, so we may be assured of the model’s decisioning capabilities at least retrospectively. This should leave us, ultimately, with a system that consumes data and recommends decisions, either on an automated or a human-in-the-loop basis.
IndexTensors
Our first innovation is “IndexTensors”. These are essentially PyTorch Tensors with Pandas indices along their dimensions. Together, they enable easy index-aligned autodiff-able operations¹. This will be easiest to see with a demo.
We begin by initializing an IndexTensors with a PyTorch Tensor, indices for each dimension and a variable name:

This is a 2-by-2 matrix with indices along each dimension. The first dimension, named ‘dim1’, has two index values ‘a’ and ‘b’. The second, named ‘dim2’, has two values ‘x’ and ‘y’. This enables, among other things, slicing by name:

The real advantage, however, is in the operations. Let’s say we had another 3-dimensional IndexTensor:

If we add them together, values are aligned by index and broadcasting is done where necessary:

In more detail, it’s as though A was copied along a third dimension identical to dim3 of B, and then added with B element-wise to yield C. C only includes values for which there are identical labels in both B and the copy-extended version of A.
More importantly, however, is that we can calculate gradients² through these operations — an essential ability when optimizing arbitrary differentiable functions. For instance, granted A has its attribute`.required_grad_ = True`, we can calculate the gradient of the sum of C with respect to A:

This tells us that the sum of C’s elements will be increased by 2 for each increase of 1 by any element of A. This makes sense since A needed to be copy-extended along dim3 to be added element-wise with B.
Taking a step back, these index aligned and autograd-able operations are what make declaring models with learnable parameters and optimizable inputs easy and flexible. These are crucial components of a modeling framework designed to produce high quality, well-vetted models.
Still, the variables-as-hypercubes³ paradigm brings other advantages. First, it necessitates aggregations. Modelers do not practically have the option of ride-level modeling because individual rides are not easily represented with a cartesian grid. However, sums of rides across regions and time are naturally represented that way.
Lastly, it easily extends into a data-store accessible by all modelers. The data-store is defined as a set of IndexTensors, one for each metric of our business (e.g. “rides”). This ensures that two modelers developing separately will pull identical data when referencing the same variables by name. This is another hard requirement for parallel model development.
The Model
We define a model as that which can predict one or more outcome variables as a function of input variables, using parameters learned from a combination of historical observations, experiments, and assumptions. We presume that this will be done, using the techniques discussed in blog 1, such that we can reasonably declare the input-output relationship “causal”.
Beyond this, a model should meet certain criteria. As previously described, each model should be modular; a model should be swappable as long as the inputs and outputs remain the same. Further, a collection of models should also count as a model. This recursion is to match the same pattern among DAGs: a collection of DAGs is a DAG itself. As such, it enables partitioning our modeling tasks into a hierarchy. We call the collection of models a ModelCollection.
Design
These desiderata can be accomplished by extending the PyTorch module structure. The PyTorch framework handles the core function: learning an input-output mapping from input-output data. It achieves this with Neural Networks in mind and as such, several components must be specified:
- Parameter initialization: how to shape and randomly initialize parameters.
- The forward function: declares the functional mapping from inputs and parameters to outputs.
- A loss function: defines the metric to optimize for selecting parameters.
- An optimizer: specifies the gradient-descent algorithm to optimize the loss and consequently select parameters.
Conveniently, PyTorch comes with a large suite of tools to make each component easy to specify, efficient and reliable. But for our purposes, it is incomplete. We extend this paradigm to enable, among other things, the aligned passage of variables across models and management/tuning of hyperparameters.
To be specific, we can reference a model collection as:

For the sake of brevity, we are now using bold capital letters to refer to sets of IndexTensors, rather than individual IndexTensors as we did in blog 1.
The Loss
One component worth expanding on is the loss function. A Model’s loss is a weighted sum of loss terms, each of which measures something we care about. These include measures of fitness, agreement with experiments (granting “causal validity”) and regularization. We can write such losses as:

As an example, si(.) could measure how well a model agrees with experimentally determined values. For example, an experiment might suggest how much ETA, the time it takes a driver to pick up a rider, will change with an 1% increase in driver hours. If the associated weight is large and the optimizer does a good job optimizing, we’ll obtain a model which agrees with whatever the experiment suggests.
As an example, below shows annotated example code of what a simple ETA model might look like:
We can see that declaring a model’s components requires relatively little code. In fact, reducing the amount of code beyond this would be difficult, if not impossible, without sacrificing model flexibility. As a point of evidence, the assortment of models we maintain heavily utilized the flexibility of each component represented here.
The ModelCollection
ModelCollections are, as their name suggests, a collection of Models. If such a collection creates no loops⁴ and thus defines a valid DAG, that collection itself counts as a Model object, since its components can be naturally inferred from the components of the models⁵. As mentioned, this enables a hierarchical strategy for partitioning the task of modeling Lyft’s business.
As an example, the following shows how simple it is to create a DAG using a collection of Models.
This means the majority of the development effort is at the individual model level, an easily distributable task. In addition, the ModelCollection-is-just-a-Model property means models can be expanded into more complex and powerful collections. For example, we could expand the sessions model to separately model coupon-induced sessions, sessions induced by weather and weather-adjusted sessions:
This ability has been critical for our gradual and incremental development of our Causal Forecasting System.
Evaluation
Beyond easy and flexible declaration of models, the ability to fairly evaluate model changes is also vital. Without it, developers are blind to the value of their changes and are bound to complexity the model without a worthwhile benefit. To this end, we introduce two main approaches:
- Causal validity. We can compare the model’s predicted outcomes against experimentally determined outcomes — this is a variable-specific approach, as we don’t always have comparable experiments.
- Predictive accuracy. Here we rely heavily on backtesting to evaluate the out-of-sample performance of the model. To simplify metrics across different variables, we largely use MASE⁶, a unit-agnostic and shift-invariant error metric.
Optimization
We embarked on this project to help Lyft make better decisions. While the models themselves will let business users at Lyft evaluate proposals, it’s a natural step to ask the model to recommend decisions directly.
To be specific, we want to make the best decisions possible with the information at hand — we’d also like to understand the impact of potential investments; e.g., whether we should invest in improving modeling and forecasting, or develop more efficient coupons
By “best decisions,” we mean we’d like to determine⁷:

As mentioned earlier, we chose to extend PyTorch for a number of reasons — one of which was the autograd functionality. In this context, it means we can efficiently calculate gradients of C though the ModelCollection, the objective function and the constraint function. Ultimately, this means we can solve the above optimization problem, even when the dimension of C is high.
As a motivating example, below we show one approach to leverage PyTorch to determine optimal decisions while obeying constraints⁸:
Evaluation
We can evaluate our decision making process as follows. We begin by introducing ex-post decisions:

That is, we will judge our decisions against decisions we would have made with perfect information of the future⁹. The first item worth expecting is the differences in our decisions:

These difference indicate the degree to which we are making bad choices due to forecast errors. It’s also worth inspecting the difference in forecasts driven by the difference in our decisions:

But these are multidimensional objects, so inspecting them may not yield clear answers on whether our decisioning process has been improved/degraded following a change. To reduce it to a single number, we inspect the difference in our objective function:
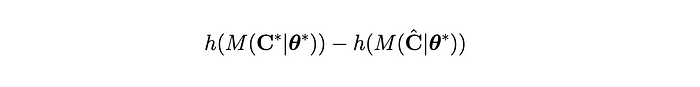
This ultimately serves as our decision rule for whether a particular change is helping or hurting. More commonly, this quantification is called the “regret¹⁰”. In code, this idea is actualized with something like:
Example Application
As a motivating example, we’ll use the aforementioned design for determining driver bonus spending. We have several driver incentive products which can induce incremental driver hours at the region-hour level.
An example driver bonus curve; increasing spend on the bonus increases the total number of incremental driver hours
Specifically, the goal is to determine how much should be spent on each driver incentive type for all region-hours. To do so, we’ve worked with our business partners to define an objective, such as maximizing the number of rides, and set constraints, such as ensuring ETAs and PrimeTime remain low and profitability guardrails aren’t violated. With this and previously described procedure, we can recommended spending.
But beyond that, we can provide context on these recommendations. For example, because we have autograd functionality, we can answer exotic questions like “what is the marginal cost per percentage point of prime time?” or “what’s the sensitivity of rides to our demand forecast?” Contextual information like this is typically reviewed before execution.
Below, we show what might be reviewed prior to execution.
With the multivariate outcomes, we can answer questions about the impact of spending decisions on a range of variables. The graphs show the impact of our decision across: ∂ETA/∂Spend, ∂PT/∂Spend, ETA, incremental driver hours (idh), prime time (pt), and number of rides. We can identify how the optimal spending decision–based on an objective function (not shown)–affects each of these metrics.
After the fact, we can rerun the process with an updated model to understand the difference between our expectations and reality. This is a retrospective analysis and provides a graphical perspective of what our regret-metric is capturing.
We can retrospectively evaluate our forecasts and decisions by comparing them to an alternative where the future is known exactly. The graphs show our forecast and actual impacts of our decision across: ∂ETA/∂Spend, ∂PT/∂Spend, ETA, incremental driver hours (idh), prime time (pt), and number of rides. This lets us observe how far we were from the actual and desired outcomes.
This provides an indication of where we should invest for decisioning improvement. Specifically, the above graph suggests our PT and ETA models are suffering large errors due to forecast error. It also suggests we spent less than we should have, consequentially producing fewer rides than we had forecast and further highlighting the cost of forecast errors.
The Big Picture
By this point, we’ve covered, from theory to implementation, our approach to a seriously hard problem: managing a complex marketplace strongly confounded by our history of decisions. The theory derives largely from graphical Causal Models¹¹ while employing news ideas for merging experimental and observational data. The implementation addresses the practical complications that arise when actualizing this theory. It enables a parallel and partitioned approach to modeling across teams, minimizes coding frictions for fast development cycles, applies judicious modeling constraints while still permitting a huge diversity of models and effectively anticipates decision optimization. The key ideas to accomplish this are to extend an existing powerful modeling framework (PyTorch), to define an index-aware and differentiable algebra over variables (IndexTensors) and to apply a consistent and honest evaluation criteria to all changes to the system.
All together, this constitutes Lyft’s Causal Forecasting System: a codebase which ingests our historical data and returns decisions we are confident in. This is not to suggest the job is done. The true complexity of our business extends well beyond that which is currently captured by the system. There remain many experimentally determined causal insights that have yet to be factored in. Nonetheless, we have a repeatable process to grow code to ultimately capture the primary mechanisms of our business. It is a process we are happy to repeat.
We’re grateful to the leadership at Lyft for continuing to invest in Lyft’s Causal Forecasting System, our partners in engineering, finance, and operations for working with us to implement these models, and the Lyft science community for continuing to build out this technology.
Footnotes
[1] For more context and motivation, see here.
[2] See this tutorial for more information on PyTorch’s autodiff functionality.
[3] See here for more details on these objects.
[4] For example, it’s invalid to have two models: A -> B and B -> A.
[5] It should be noted that, even though the required components may be inferred from the constituent models, it often helps to tailor the components directly for the ModelCollection. In particular, a ModelCollection’s fit routine can be improved beyond merely running the fit routine of the models.
[6] Mean Absolute Scaled Error (MASE)
[7] To keep notation simpler, blog 1 did not use constraints. Instead it incorporated constraints as soft-constraint penalties in the objective function.
[8] In this example, constraints are met using Projected Gradient Descent.
[9] This is not to suggest all sources of error are eliminated with the ex-post decisions. Other sources of errors include errors in modeling assumptions and measurement mechanics.