lyft2vec — Embeddings at Lyft
Co-authors:
, and
Intro
Graph learning methods can reveal interesting insights that capture the underlying relational structures. Graph learning methods have many industry applications in areas such as product or content recommender systems and network analysis.
In this post, we discuss how we use graph learning methods at Lyft to generate embeddings — compact vector representation of high-dimensional information. We will share interesting rideshare insights uncovered by embeddings of riders, drivers, locations, and time. As the examples will show, trained embeddings from graphs can represent information and patterns that are hard to capture with traditional, straightforward features.
Lyft Data and Embeddings
At Lyft, we have semi-structured data capturing complex interactions between drivers, riders, locations, and time. We can construct graphs representing these interactions (e.g. a graph can be formed by connecting a rider with all the locations they have visited). From these graphs we can generate embeddings to succinctly express a rider’s or driver’s entire ride history. These embeddings allow us to efficiently summarize vast and varied information in a machine-friendly representation.
For example, there are over 9,000 Geohash-6 (Gh6) level locations around the San Francisco Bay Area. If we wanted to describe a driver’s ride history around the Bay Area without embeddings, we would need a histogram or vector of length over 9,000 to describe it precisely. The vector would contain the number of rides the driver has started in each Gh6, with lots of zeros if the driver has never been in some Gh6s.
With graph learning we are able to train a lower dimensional embeddings vector that represents the same information. It may not capture the exact details due to the inherent dimension reduction, but as we will show in Lyft Ride Insights below, well-trained embeddings are able to capture the overall picture of a driver’s travel history.
Another benefit is that embeddings are d-dimensional vectors which describe single points in a d-dimensional vector space and those spaces can be shared by different defined entities. Entities are the points, or nodes, in the input graph that we want to be represented by embedding vectors and are grouped together by entity types. For instance, we can construct two embedding vectors, one representing a rider entity and one representing a location entity from the same graph, where a connected edge in the graph means this rider has visited this location. With a similarity function (defined in the problem setup), we can directly compare the two embedding vectors by calculating a similarity score between them. In this graph, the similarity score would describe how frequently our rider has visited this chosen location.
While a graph can incorporate many different entity types (e.g. rider, location, driver) and relationships (e.g. picked up, dropped off), simple graphs can still be informative. As our examples will show, even with just two entity types and one type of relationship, graph-based embeddings can still give valuable insights.
Methodology
A multi-entity graph is constructed by drawing entities as nodes and making connections (i.e. edges) between entities where there is an interpretable relationship. The idea of graph-based embeddings is to encode nodes so that similarity in the embedding space (e.g. dot product) approximates closeness in the graph. Two entities have a high similarity score with their embeddings if they are either directly connected in the original graph (i.e. “1-degree” connection distance), or have a very close distance (i.e. “2-degree” connection).
There are two key components: 1) an encoder which maps each node to a low-dimensional vector and 2) a similarity function which specifies how the relationships in the vector space map to the relationships in the original network.

Figure 1: An Illustration of Graph Embeddings¹
We can specify the dimensions of the embeddings (i.e. output) space in the training process. By choosing an appropriate dimensionality, we are able to capture the intricate relationships between entities from the original input graph in a much lower and compact dimensional vector space. We can even do distance calculations with vector dot products in the embeddings space to get a quantitative measure of the “similarity” or “distance” between different entities.
Next, we will use a simple Lyft ride graph as an example to illustrate the details of embeddings training.
Ride Graphs at Lyft and Embeddings Training
At Lyft, we are interested in learning about riders, drivers, and their ride preferences with respect to factors such as location and time.
Taking location as an example, we can construct a graph like Figure 2. Each rider, driver, and location is represented as a separate entity, and connections are drawn where a rider or driver has started a ride from a certain location.

Figure 2: An Example of Ride Graph
Our training algorithm extends from the Pytorch BigGraph package. At the beginning of training, we specify the d dimensions of embedding vectors we want to obtain, and the algorithm assigns random values to these d-dimensional embedding vectors as initial parameters. As a general principle, we choose a higher output embedding dimension if the original graph is complex with a large number of entities and intricate connected edges. A higher embedding dimension will capture more information from the graph.
The goal of training is to learn d-dimensional embedding vectors for each entity (i.e. node) such that the calculated similarity between any two entities reflects their relationship. For example, two entities that are very close in the space would have a more positive similarity score than two distant entities.
During each training cycle, for each entity, every edge connected to the entity in the original input graph is considered a positive (+) instance, while the algorithm randomly samples from the unconnected entities for negative (-) instances. In our ride graph, the samples would look like Figure 3 below. Notice how positive labeled edges exist in Figure 2 above, but negative labeled edges do not.

Figure 3: Ride Graph in Training with Positive and Negative Instances
The embedding vectors for entities are pairwise compared using a chosen comparator to generate a similarity score. A simple choice is cosine similarity, which is calculated as the dot product of two vectors.
Once the scores of all the positive and negative samples have been determined, a loss metric aggregates the scores into a single loss value per epoch to enable learning. Common loss function are ranking loss, logistic loss, and softmax loss.
Lastly, the loss is minimized using an Adagrad optimization method to update all model parameters.
Lyft Ride Insights
Now we can show interesting insights that ride graph embeddings revealed. A quick disclaimer that our analysis focuses on anonymous or aggregated information and we do not aim to derive any personal characteristics or insights about our riders and drivers from the learned embeddings.
Driver Ride Pattern Comparison
The first example will show how embeddings can compactly capture rich high dimensional information. As a fun exercise, we construct a graph exploring different location patterns of drivers around the Bay Area.
The input is a graph with Driver and Gh6 as entities, and edges connecting a driver and a ride’s pickup Gh6 for each requested ride during several months time (i.e. the embeddings training period). The output is a 32-dimensional embedding for each Gh6 location and for each driver.
With the embeddings, we calculated the similarity between every pair of driver and Gh6. In this example, similarity would signal how frequent a driver has picked up rides from a Gh6 location. The higher the similarity score is, the more rides a driver has picked up from that location.
We picked two drivers — driver A and B, and calculated the similarity score of every Gh6 with them through the dot product of their embeddings. Figure 4 shows the similarities of every Gh6 to Driver A and Driver B, respectively with higher scores having darker shades.
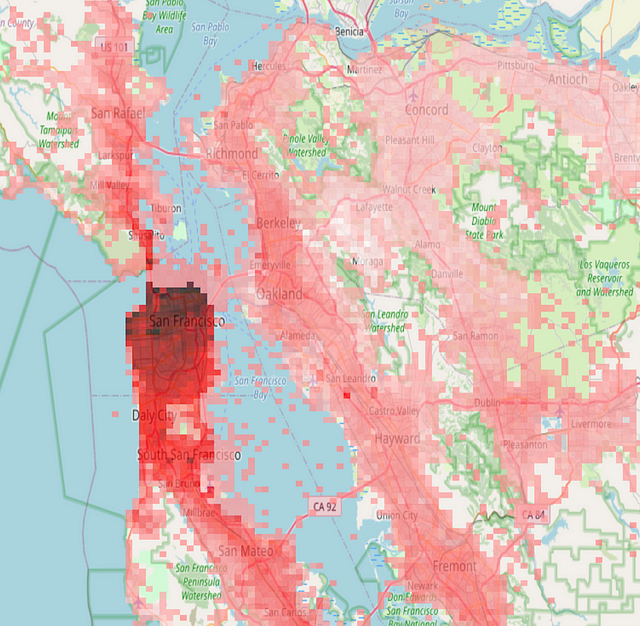

Figure 4: Similarities of Two Drivers to Locations around the Bay Area
From the similarity plots, we can clearly visualize the distinct ride patterns of the drivers. We see that Driver A (left panel) is a SF City Driver. They sometimes drive a little down south for rides in the Peninsula area or a little up north for rides in the North Bay area, but they rarely go to the East Bay or South Bay areas.
In contrast, Driver B (right panel) is primarily an East Bay Driver who has picked up more rides in the Fremont area where the darkest shades concentrate. They sometimes drive to the Peninsula area of South Bay via the bridges, but rarely go to the San Francisco city area.
These interesting ride patterns could require a large histogram of ride frequencies with respect to locations to describe. With embeddings, we are able to get a very rich picture of the drivers’ ride patterns with just a 32-dimensional vector!
Ride Patterns Throughout the Week
In the next example, we will show how using temporal embedding features can help uncover hidden relationships and insights that may not be obvious with simple time features such as hour of day or hour of week.
We constructed a graph with Driver and hour of the week as entities, and edges connecting a driver and an hour of the week for each ride the driver picks up that starts during that hour. The output was a simple four-dimensional embedding for each hour of the week and for each driver. We only used four-dimensional embedding vectors since there are just 168 hour-of-the-week entities compared to thousands of Gh6s in the previous example. With this graph, we can compare the similarity between every hour of the week to every other hour of the week and observe ride patterns through the week.
We picked two reference hours — Saturday at 8 p.m. and Monday at noon local time in all regions in the U.S. and calculate the similarity score of every hour-of-the-week with them. These two reference hours are chosen because they represent very distinctive ride patterns.


Figure 5: Similarities of Saturday 8 p.m. and Monday 12 p.m. to Other Hours of the Week
On the left plot of Figure 5, the hump a little before “x = Su” shows that Saturday 8 p.m. has the highest similarity score to itself, which is expected. What is interesting is that the next most similar hours to Saturday 8 p.m. appear to be Friday 8 p.m. followed by 8 p.m. on Sunday. The next most similar are Monday through Thursday at 8 p.m., though they are distinctively at lower similarity level than 8 p.m. on Friday.
When Monday at 12 p.m. is the reference time a different picture emerges. The right plot of Figure 5, is most similar to Monday through Friday at noon, and less similar to Saturday or Sunday at noon.
What does this mean? Based on our construction of the graph that includes drivers and hour-of-week as entities, similar in that case may be interpreted slightly differently. An interpretation could be that drivers who are more similar to an hour of week have given more rides at that time.
With a simple contrast of these two plots, we can almost pick out distinctive driver and ride groups on the Lyft platform — the weekend “party-hour” drivers and rides vs. the weekday “commute-hour” drivers and rides. This information is all represented in the 4-dimension vectors for each hour of week that can be easily fed as input into a model. Through embeddings we are able to elegantly capture and convey this hidden relationship we would have missed if we had only used hour of week as a feature!
What’s Next
After seeing several successful applications of embeddings, we are building a platform to empower many machine learning (ML) modelers at Lyft to utilize them. The approach to construct data graphs and build embeddings is very flexible and can be applied to study the various intricacies of the Lyft rideshare business. The insights uncovered can help us understand different ride patterns, marketplace dynamics, and ultimately build better products and ride offerings for our riders and drivers.
In the scope of an Embeddings Platform initiative, many distinct modeling projects are supported to build custom embeddings and use them as innovative features in ML models. We are concurrently solving problems with data and feature quality, automated retraining, governance, compliance, and training-serving infrastructure for our supported teams.
We plan to maintain fresh embeddings for the most interesting entities in the Lyft marketplace and make them available as easily accessible features for many common use cases.