Causal Forecasting at Lyft (Part 1)
By Duane Rich and Sameer Manek
Efficiently managing our marketplace is a core objective of Lyft Data Science. That means providing meaningful financial incentives to drivers in order to supply affordable rides while keeping ETAs low under changing market conditions — no easy task!
Lyft’s tool chest contains a variety of market management products: rider coupons, driver bonuses, and pricing, to name a few. Using these efficiently requires a strong understanding of their downstream consequences — everything from counts of riders opening the Lyft app (“sessions”) to financial metrics.
To complicate the science further, our data is heavily confounded by our previous decisions, so a merely correlational model would fail us. Sifting out causal relationships is the only option for making smart forward looking decisions.
In two blog posts, we’ll explain our solution, an internal product we will refer to as Lyft’s “Causal Forecasting System¹”. The first (this post) will discuss the business problem, basic principles and modeling techniques. The second will describe our software used to actualize these ideas and apply them at scale. In doing so, we’ll cover our use of causal inference, causal modeling, and PyTorch to develop a large model, containing Lyft’s consensus view of our business, which ultimately drives large capital allocating decisions. Let’s begin!
The Task
Lyft is internally organized around product-focused teams. These include teams focused on driver bonuses, rider coupons, pricing, and activating new drivers. Each is primarily focused on metrics directly tied to their products. For example, the rider coupon team tries to increase the number of active riders and total rides by cost effectively targeting riders with coupons.
For our purposes, it’s useful to think of a team as a function which optimizes their metrics based on given inputs. A typical example of an input is a weekly spending budget. Though, it could be something stranger, like an average ride price. This leads to the question: how are these inputs determined? Doing so constitutes a “policy decision”, and choosing them well is the system’s primary purpose.
To be precise, let V₁, V₂, …, Vₖ be variables that represent our key business metrics and let C₁, C₂, …, Cₗ be variables we control (“policy variables”). For example, V₁ and V₂ could be ride counts and revenue respectively, while C₁ could be the rate card². Our goals are to:
- Build a model which accurately forecasts V₁, V₂, …, Vₖ when given policy variables.
- Given the model, determine the policy values which optimize some metric of the forecasted variables.
As we’ll demonstrate, with the right set of variables, performing these tasks well enables intelligent organization-level decisions. At the same time, they present significant technical challenges well beyond what one would expect with correlational forecasting.
Causal Modeling
Our approach is heavily inspired by causal models³. In particular, we assert each variable is caused by some set⁴ of other variables, and therefore we can predict the former from the latter. It turns out such a statement can be represented as a “Directed Acyclic Graph” which is a graph of nodes and edges without loops⁵. For the purposes of causality, each variable is a node with a directed edge from any variable that causes it.
For example, let’s say the average price shown to a user and conversion, the proportion of sessions which convert to rides, are two of our variables. We’ll assume conversion is caused by price, which may be represented as a DAG:

To emphasize, this graph encodes the assumption “conversion is caused by price and nothing else.” Next, let’s assume rides are generated as the product of sessions and conversion:

This may be combined with our previous DAG to yield a larger one:

This gives us a means of combining assumptions such that we can relate all variables of our business, and is suggestive of a divide-and-conquer modeling strategy. Since a combination of causal models yields another larger causal model, we can decompose our task into small modeling tasks. A benefit of this is a type of modeling parallelism. Data scientists can model independently to yield a large graph representing a consensus view of the business.
Yet, our strategy goes beyond merely encoding causal statements. At Lyft, we use experiments to evaluate such connections. Specifically, they’re used to inform the functional relationship between policy decisions and outcomes.
Driver Incentives
One motivating example is driver incentives and their impact on driver hours, which can be represented as:

Some plausible synthetic data of driver incentive budget and driver hours can be represented as two time series on the left and a scatter plot on the right:
It’s clear that any correlational model will pick up on the scatter plot’s negative correlation. To demonstrate, we can show the predictions of one such model⁶:
The problem with this is the implied differential relationship between budget and driver hours. To see that, for a specific date, we vary the budget and observe the difference in driver hours (“incremental driver hours”):
This suggests that for any budget above ~60K, driver hours can be increased by decreasing driver incentive budget — obviously wrong! Clearly, this model cannot be used for planning.
One way to address this is to import an experimentally determined “cost curve” from the driver bonus team and create a model which obeys that differential relationship. Such a cost curve might look like:
With this, we can develop a model⁷ which produces similarly accurate predictions while matching the cost curve exactly:
Now we are in a good position. Our model forecasts accurately and can be used for decisioning since it matches what the driver bonus team believes will change as their budget changes.
Combining Models
This example is illustrative of a principle that can be applied repeatedly; encode causal assumptions as a DAG, import some empirical, ideally experimental, relationships and develop a model which matches those while fitting historical data. Roughly, we think of our observed data as something to fit while experiments suggest how outputs change if we change our decisions⁸. And with software to be discussed later, this principle can yield a large and diverse set of models. Stitching them together can yield a comprehensive model which represents our data and assumptions and is valid to use both for forecasting and planning. To illustrate, it’s rather easy to generate a model like:
A read of this DAG communicates the function of our business. More importantly, if our assumptions are correct, our causal relationships are accurate and the models are predictive, this model collection accomplishes tasks 1). The inputs are our control variables and the outputs are everything downstream.
Planning and Optimization
Getting back to our initial raison d’être, we can use this model to make forecasts conditional on our decisions, what we’ll call a plan. With it, decision makers can, for example, evaluate the tradeoffs between pursuing a balanced vs aggressive growth strategy as shown below:
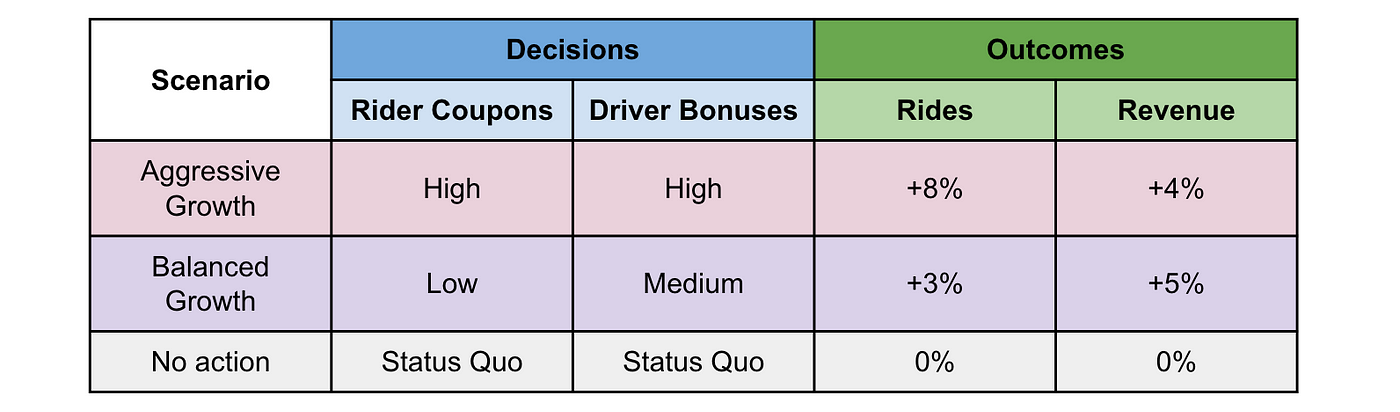
This is to suggest that completing task 1 is useful in and of itself. Indeed, we have UI’s at Lyft which enable interacting with the model directly.
With the ability to model different scenarios, we can naturally use our models to optimize for specific goals, task 2. For example, we maximize “total rides subject to a revenue-per-ride constraint”, which we can express as scalar function⁹:
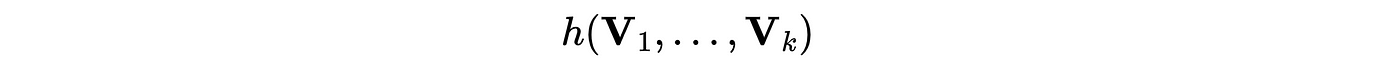
As mentioned, we can predict these variables with our model:
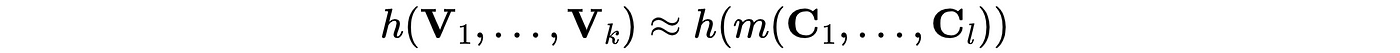
where m(.) indicates our model. From here, our goal is to optimize this with respect to our policy variables:
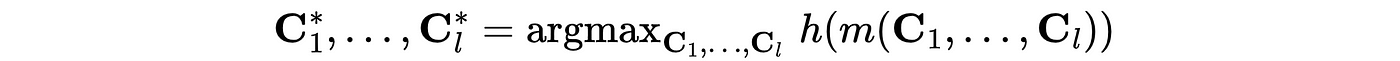
With a few assumptions and limitations, this is a tractable high dimensional optimization problem — something we’ll address in the next post.
What’s Next?
In order to make decisions efficiently and scalable at Lyft, we’ve developed a large causal model — that is, a model that is both predictive and causally valid, and composed of smaller models. This model collection allows product-focused teams to focus on metrics within their control, embeds our understanding of the marketplace, and allows decision makers to make informed decisions. Beyond that, the model has been designed with optimization of decisions in mind.
In the next post, we’ll discuss our solutions to problems that remain:
- How can models be quickly yet flexibly declared?
- What software is used to enable independent modeling yet a seamless integration of those models?
- How are plans, especially high dimensional ones, optimized?
Footnotes
[1] Internally, we use a different name.
[2] The Rate Card determines how much a rider is charged per minute and per mile.
[3] Causal Models (Stanford Encyclopedia of Philosophy)
[4] This subset could be the empty set, in which case predicting that variable would be a forecasting task dependent on no other variables.
[5] A loop is a path like A → B → C → A. We exclude them because they prevent us from determining which variables should be predicted before which other variables.
[6] The model smooths the input budget and applies a polynomial regression.
[7] Specifically, the model uses the cost curve directly to model how budget impacts driver hours and then uses a smoothly evolving moving average to model the residual. This is analogous to adding covariates to a forecast (e.g., ARIMAX models are an extension of ARIMA models to incorporate exogenous variables). The fact that the model needs to be more complex to maintain predictability and match the cost curve is a pattern that appears frequently when faced with both goals.
[8] However, since two observed data points are also suggestive of how things change, a model often must trade off how well it matches observations vs experiments. In general, complex models are more capable of matching both than simpler ones.
[9] It’s implied that the constraint is included within the function as a soft constraint.